[TIL]4.Basic Derivative
목표
- 최적와와 미분의 관계
- 미분, 편미분, Chain Rule의 차이를 이해
- 도함수(미분)을 파이썬으로 직접 구현 및 scipy 라이브러리를 활용
미분(Derivative)

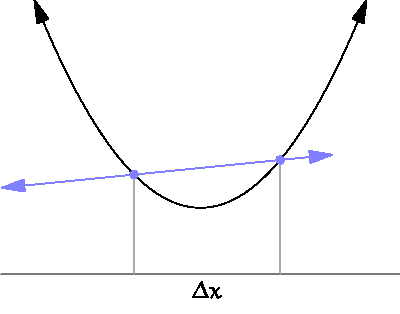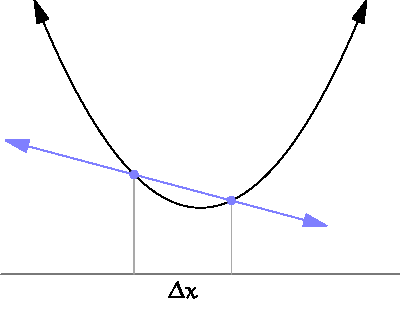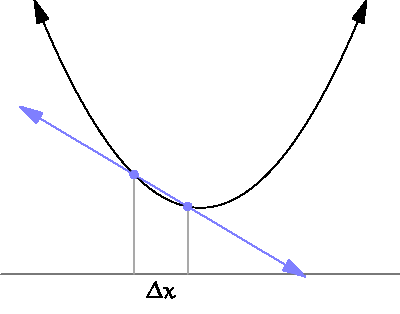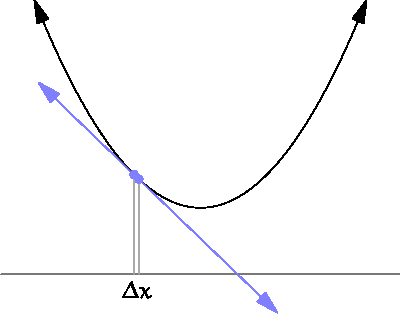
그림을 보면 우리가 계산하고자 하는 것은 Δx가 한없이 0에 가까워질 때의 기울기
특정한 파라미터 값 (input, x)에 대해서 나오는 결과값(output, y)이 변화하는 정도를 (0에 가까운 부분을 찾기 위해) 계산하는 것.
미분과 데이터 사이언스는 무슨 상관이 있나?
아래와 같은 데이터 분포가 있을 때, 그 분포를 가장 잘 설명해주는 하나의 선을 그린다고 생각해보자.
y-hat=b+aX (a:기울기, b:y절편, y-hat:예측값, x:데이터) cf) 보통 실제값은 그냥 y로 표현한다.
주어진 데이터 X를 넣었을 때, 모델이 예측하는 예측값과 실제값 간의 차이(Error, ε)를 계산, 여러 모델 중 Error(모델에서 예측하는 예측값과 실제값 (y)의 차이)가 가장 작은 모델을 선택하는 방법을 통해 가장 좋은 모델을 선택한다링.
이를, f(a,b)=ε 로 표현 될 수 있으며, 오차 함수인 ε을 최소화 하는 a,b를 찾는 것이 머신러닝(Linear regression)의 목표!!!
이때, 선형회귀모델의 경우 오차 함수는 보통 'Mean Squared Error'를 사용!!
즉, 우리가 2차 함수의 기울기가 0일 때를 포물선의 끝점(y값이 최소가 되는 지점)을 찾듯이 f(a,b)를 미분하여 Error가 최소되는 a,b를 찾는 것 => Mean Squared Error
Numerical method를 이용한 미분 계산(보통 델타x를 1e-5(아주 작은 값)을 넣어서 수식을 통한 계산)
def f(x):
return 3*(x**4) + 10
def numerical_derivative(fx, x):
delta_x = 1e-5
return (fx(x + delta_x) - fx(x)) / delta_x
numerical_derivative(f, 2)scipy를 이용한 미분 계산(사기임)
from scipy.misc import derivative
drivative(f, 2, dx=1e-5)cf) 허나 실제로 위 두 값을 비교해보면 False가 나온다. 이유 : delta x 값이 같은데, python의 rounding 에러로 인해 두 결과가 미묘하게 다름(참고만 하자)
편미분(Partial Derivative) 라운드로 표기
많은 머신러닝의 Error 함수는 여러 가지의 파라미터를 통해 결정된다.
파라미터가 2개 이상인 Error 함수에서 '우선 1개의 파라미터에 대해서만 미분을 하자'라는 목적으로 하는 미분
간단히, 다른 독립변인(파라미터)를 상수취급해서 미분하는 것. (차원이 커질 땐 방향에 따라서 미분 기울기가 달라지니까)
Chain Rule
F(x)=f(g(x))
F′(x) → f′((g(x))⋅g′(x)
Chain Rule은 딥러닝의 핵심 개념 중 하나인 Backward Propagation(역전파)을 이해하는데 중요하니 기억해두자 :)
경사하강법(Gradient Descent; GD)
위에서 거론된 오차 함수(𝜀)를 최소화하는 a,b를 찾을 수 있는 최적화 알고리즘 중 하나!
최적의 a,b를 찾기위해선 미분계수가 0인 값을 찾아야한다. 그러나 현실적으로 우리가 다룰 문제는 파라미터의 개수가 수없이 많고
또한 하나의 minimum/maximum만 존재하는 게 아닐 것이다.(단순 2차함수가 아니니까)
해서 경사하강법은 임의의 a,b를 선택한 후(random initialization), 기울기(gradient)를 계산해서 기울기 값이 낮아지는 방향으로 계속 진행
기울기는 항상 손실 함수 값이 가장 크게 증가하는 방향으로 진행한다. 따라서 경사하강법 알고리즘은 기울기의 반대 방향으로 이동
경사하강법에서 a,b는 다음과 같이 계산 됩니다 :
a[n+1]=a[n] −η∇f(a[n])
b[n+1]=b[n] −η∇f(b[n]) => 그래디언트와 반대로 가니까 앞에 - 부호가 붙는다.
이렇게 반복적으로 파라미터 a,b를 업데이트해가면서 그래디언트(∇f)가 0이 될 때까지 이동!! (a[n]과 a[n+1]이 차이가 없을 때까지)
이 때, η(에타, 여기선 learning rate; 학습률)가 중요! 너무 낮게 되면 수렴하는데 너무 많은 시간이 걸리고, 너무 크면 오히려 극소값을 지나쳐 버려서 알고리즘이 수렴하지못하고 발산해버림
- 경사하강법은 추후에 더 자세히 배울테니 개념 정도를 알고 있도록!!!
(사이트가 기억 안나는데, 경사하강법 파라미터 정해두고 직접 시각적으로 보게 해주는 사이트 기억!)
여기라도 참고하자 [https://uclaacm.github.io/gradient-descent-visualiser/]