목표
- 머신러닝모델링 시 train/test 데이터 분리해야하는 이유를 알기
- 다중선형회귀 이해
- '일반화' 관점에서 과적합 및 과소적합 이해
- '일반화' 관점에서 편향 및 분산의 트레이드 오프 개념 이해
train/test 데이터 나누기
- 데이터를 훈련/검증 데이터로 나누어야 우리가 만든 모델의 에측 성능을 제대로 평가 가능
- 모델링의 목적은 'train data'를 잘 맞추는 것이 아니라, 훈련에 사용하지 않는 'test data'를 이용해서 얼마나 정답을 내느냐
나누는 방법엔 다양한 방법이 있지만 우선 아래와 같은 방법이 있다.(train이 75%, test가 25%)
train = df.sample(frac=0.75, random_state=1)
test = df.drop(train.index)주의점 : 일반적으로 데이터를 무작위로 선택해서 나눠도 괜찮지만, 시계열 데이터를 통해 과거에서 미래를 예측하려고 하는 경우엔 무작위로 데이터를 선택하면 안될 것이다. 이 때는 과거 데이터가 train , 미래가 test 가 되어야할 것이다.
다중선형회귀모델 학습(예시를 들고 진행)
- 기준모델(특성X)
- 다중선형회귀모델
import pandas as pd
df = pd.read_csv('https://ds-lecture-data.s3.ap-northeast-2.amazonaws.com/house-prices/house_prices_train.csv')
train['SalePrice'].mean()
target = 'SalePrice'
y_train = train[target]
y_test = test[target]
predict = y_train.mean()
# 기준모델로 훈련 에러(MAE) 계산
from sklearn.metrics import mean_absolute_error
y_pred = [predict] * len(y_train) # 평균값의 리스트 원소를 1095개만큼 만들어주는 작업
mae = mean_absolute_error(y_train, y_pred)
# 테스트 에러(MAE)
y_pred = [predict] * len(y_test)
mae = mean_absolute_error(y_test, y_pred)위를 통해 기준모델에 대한 평가 가능
target = 'SalePrice'
features = ['GrLivArea', 'OverallQual'] # 꼭 target과 features를 먼저 지정해두기
X_train = train[features]
X_test = test[features]
# 모델 fit(train에 대해)
model.fit(X_train, y_train)
y_pred = model.predict(X_train)
mae = mean_absolute_error(y_train, y_pred)
# test에 대해
y_pred = model.predict(X_test)
mae = mean_absolute_error(y_test, y_pred)plotly를 통해 위의 경우를 시각화해본 사진입니다.
단순선형회귀에서는 모델이 직선이지만, 여기선 특성이 2개이므로 평면으로 표현됩니다.

회귀계수 해석 및 모델 평가
- 단순선형회귀식 : $$y = \beta_0 + \beta_1 x $$
- 다중선형회귀식(특성 2개) : $$y = \beta_0 + \beta_1x_1 + \beta_2x_2$$
## 절편(intercept)과 계수들(coefficients)
model.intercept_, model.coef_(-102743.02342270731, array([ 54.40145532, 33059.44199506]))
회귀계수들을 보고 target과 feature의 관계를 어느정도 유추 가능
선형회귀는 다른 ML 모델에 비해 상대적으로 학습이 빠르고 설명력이 강함. 하지만 선형 모델이므로 과소적합(underfitting; 학습이 충분히 못일어나는 경우)이 잘 일어나는 단점
회귀모델 평가지표(Evaluation metrics, 중요)
- MSE (Mean Squared Error) =
$$\frac{1}{n}\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}$$ - MAE (Mean absolute error) = $$\frac{1}{n}\sum_{i=1}^{n}\left | y_{i} - \hat{y_{i}} \right |$$
- RMSE (Root Mean Squared Error) =
$$\sqrt{MSE}$$ - R-squared (Coefficient of determination) =
$$1 - \frac{\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}}{\sum_{i=1}^{n}(y_{i} - \bar{y_{i}})^{2}} = 1 - \frac{SSE}{SST} = \frac {SSR}{SST}$$ - 참고
- SSE(Sum of Squares
Error, 관측치와 예측치 차이): $$\sum_{i=1}^{n}(y_{i} - \hat{y_{i}})^{2}$$ - SSR(Sum of Squares due to
Regression, 예측치와 평균 차이): $$\sum_{i=1}^{n}(\hat{y_{i}} - \bar{y_{i}})^{2}$$ - SST(Sum of Squares
Total, 관측치와 평균 차이): $$\sum_{i=1}^{n}(y_{i} - \bar{y_{i}})^{2}$$ , SSE + SSR
- SSE(Sum of Squares
R^2외에 MAE는 단위 유닛이 같으므로 보다 해석에 용이한 장점이 있고, MSE는 제곱을 하기 때문에 이상치에 보다 민감
RMSE는 이런 MSE의 단점을 루트를 씌워 보완한 것입니다.
과적합(Overfitting)과 과소적합(Underfitting)
일반화(generalization)
- test data에서 만들어내는 오차를 일반화 오차입니다.
- 일반화가 잘된 모델 : train data에서와 같이 test data에서도 좋은 성능을 내는 모델
- 과소적합보단 과적합(모델이 train set에 과하게 학습된 경우)이 더 자주 있고 이를 해결하기 위한 다양한 일반화 방법이 존재
- test data에서 오차가 적게 나오는 게 이상적, 그러나 현실적으로 모든 data를 얻을 수 없기에 train data로부터 최대한 일반화가 잘 된 모델을 학습시켜야합니다.
과적합(Overfitting) : 모델이 train data의 성질에 과하게 학습해서 test data에서는 오차가 커지는 현상
과소적합(Underfitting) : 모델이 train data에 학습하지 못해, 결국 train/test data 모두에서 오차가 큰 경우
머신러닝 과정 중에서 과적합은 피할 수 없는 문제이고 완전히 극복할 수 없다. 해서 대부분 학습알고리즘은 이런 과적합을 완화시킬 수 있는 방법을 제공합니다.
분산(Variance)과 편향(Bias)
위의 과적합/과소적합과 연관
- 분산이 높은 경우(편향이 낮은 경우) : 모델이 train data의 noise에 민감하게 적합하여 test data에 일반화를 못한 경우 즉, 과적합
- 편향이 높은 경우(분산이 낮은 경우) : 모델이 train data의 특성 및 타겟 변수의 관계를 잘 파악하지 못한 경우 즉, 과소적합
MSE를 reducible과 irreducible error로 나눈면 결국 Bias error 와 'Variance + irreducible error' 로 나누게 됩니다.
$${\displaystyle \operatorname {E} _{D}{\Big [}{\big (}y-{\hat {f}}(x;D){\big )}^{2}{\Big ]}={\Big (}\operatorname {Bias} _{D}{\big [}{\hat {f}}(x;D){\big ]}{\Big )}^{2}+\operatorname {Var} _{D}{\big [}{\hat {f}}(x;D){\big ]}+\sigma ^{2}}$$
$${\displaystyle \operatorname {Bias} _{D}{\big [}{\hat {f}}(x;D){\big ]}=\operatorname {E} _{D}{\big [}{\hat {f}}(x;D){\big ]}-f(x)}$$
$${\displaystyle \operatorname {Var} _{D}{\big [}{\hat {f}}(x;D){\big ]}=\operatorname {E} _{D}[{\big (}\operatorname {E} _{D}[{\hat {f}}(x;D)]-{\hat {f}}(x;D){\big )}^{2}]}$$
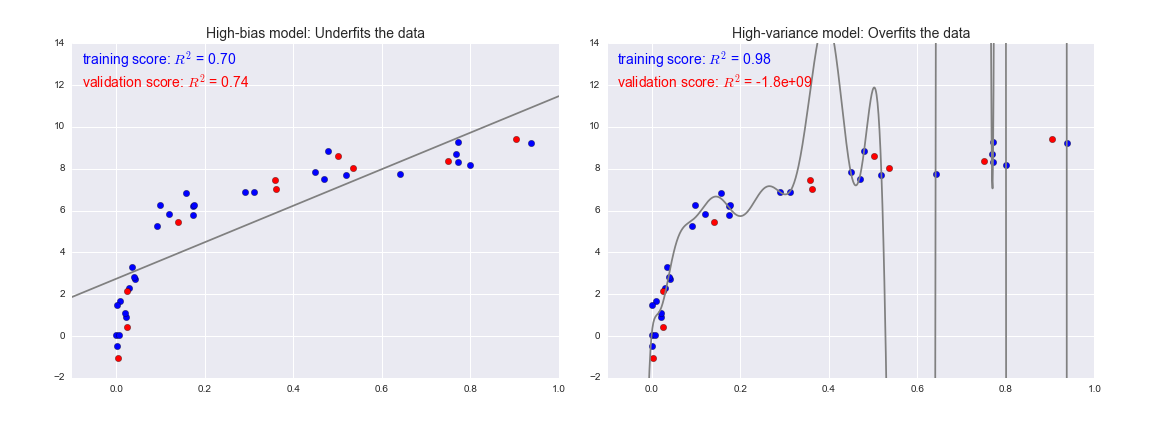
예시
왼쪽 : 단순선형모델로 학습한 경우
오른쪽 : 데이터 포인트를 모두 지나가도록 곡선 피팅이 가능한 다항모델로 학습한 경우(모델의 복잡도가 좀 더 높은 경우)

왼쪽의 경우, train data의 target과 오차가 큼 == '편향이 높음' 그러나, test data의 target과도 오차가 있어서 두 데이터에서의 오차가 비슷함 == '분산이 낮음' -> 과소적합
오른쪽의 경우, train data의 target과 오차가 작음 == '편향이 낮음' 그러나, test data의 target과는 오차가 매우 커서 두 데이터에서의 오차가 매우 차이남 == '분산이 높음' -> 과적합
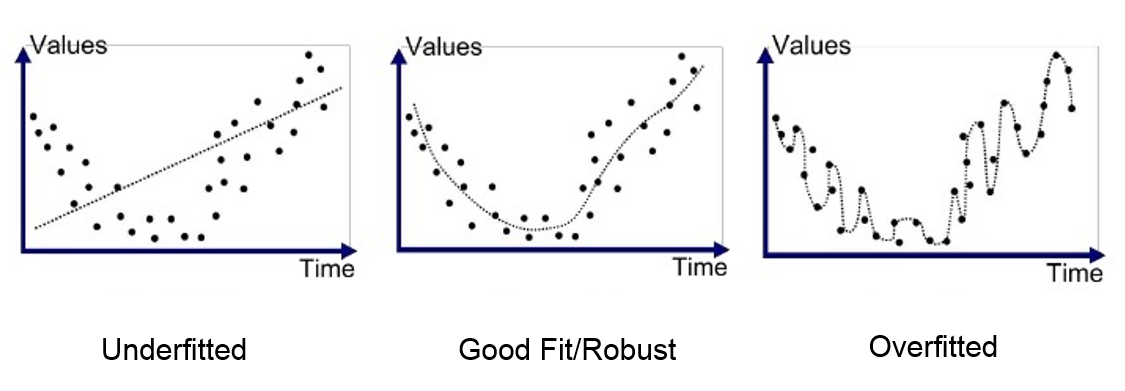

만들기 쉽지 않지만, 편향도 적고 분산도 적은 모델이 제일 best
어떤 모델을 학습시키든 train/test data 에서의 모델 성능과 그 차이를 보고 과적합 및 과소적합을 적적하게 구분해 낼 수 있는 것이 중요합니다.
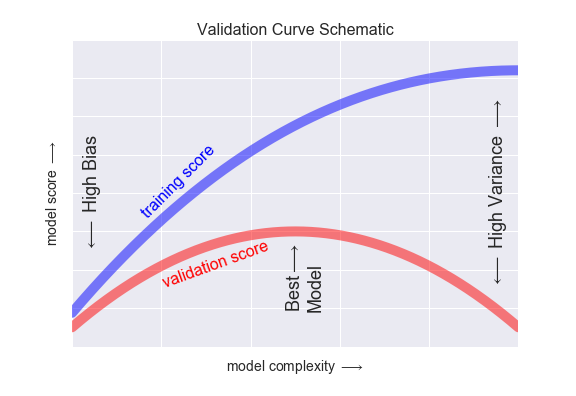
모델이 복잡해질수록 train data에서의 성능은 계속 증가하는데, 검증데이터(여기선 test data로 하자)에서의 성능은 증가하다가 감소하는 지점이 발생합니다. 이 지점이 과적합이 시작되는 시점으로 더 복잡한 모델을 학습시킬 필요가 없어집니다.
'💿 Data > 부트캠프' 카테고리의 다른 글
| [TIL]26.Logistic Regression(로지스틱 회귀; 분류) (0) | 2021.12.22 |
|---|---|
| [TIL]25.Ridge Regression(능형 회귀) (0) | 2021.12.21 |
| [TIL]23.Simple Regression(단순회귀) (0) | 2021.12.18 |
| [TIL]22.Section Challenge 및 복습 (0) | 2021.12.17 |
| [TIL]21.Session 복습 (0) | 2021.12.16 |